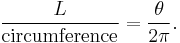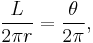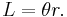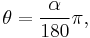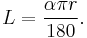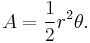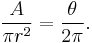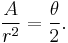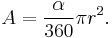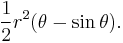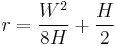Arc (geometry)

In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle. If the arc is part of a great circle (or great ellipse), it is called a great arc.

1 Arc length
2 Arc area
3 Arc segment area
4 Arc radius
5 See also
6 External links

Arc length

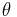The length of an arc of a circle with radius $r$ and subtending an angle $\theta\,\!$ (measured in radians) with the circle center — i.e., the central angle — equals 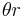$\theta r\,\!$ . This is because

$\frac{L}{\mathrm{circumference}}=\frac{\theta}{2\pi}.\,\!$

Substituting in the circumference

$\frac{L}{2\pi r}=\frac{\theta}{2\pi},\,\!$

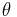and solving for arc length, $L$ , in terms of $\theta\,\!$ yields

$L=\theta r.\,\!$

An angle of $\alpha$ degrees has a size in radians given by

$\theta=\frac{\alpha}{180}\pi,\,\!$

and so the arc length equals

$L=\frac{\alpha\pi r}{180}.\,\!$

A practical way to determine the length of an arc in a circle is to plot two lines from the arc's endpoints to the center of the circle, measure the angle where the two lines meet the center, then solve for L by cross-multiplying the statement:

measure of angle/360 = L/Circumference.

For example, if the measure of the angle is 60 degrees and the Circumference is 24", then

60/360 = L/24

360L=1440

L = 4".

This is so because the circumference of a circle and the degrees of a circle, of which there are always 360, are directly proportionate.

Arc area

The area between an arc and the center of a circle is:

$A=\frac{1}{2} r^2 \theta.$

The area $A$ has the same proportion to the circle area as the angle $\theta$ to a full circle:

$\frac{A}{\pi r^2}=\frac{\theta}{2\pi}.$

We can get rid of a $\pi$ on both sides:

$\frac{A}{r^2}=\frac{\theta}{2}.$

By multiplying both sides by 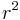$r^2$ , we get the final result:

$A=\frac{1}{2} r^2 \theta.$

Using the conversion described above, we find that the area of the sector for a central angle measured in degrees is:

$A=\frac{\alpha}{360} \pi r^2.$

Arc segment area

The area of the shape limited by the arc and a straight line between the two end points is:

$\frac{1}{2} r^2 (\theta - \sin{\theta}).$

To get the area of the arc segment, we need to subtract the area of the triangle made up by the circle's center and the two end points of the arc from the area $A$ . See Circular segment for details.

Arc radius

Using the equality in the intersecting chords theorem (also known as power of a point or secant tangent theorem) it is possible to calculate the radius $r$ of a circle given the height $H$ and the width 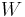$W$ of an arc using:

$r=\frac{W^2}{8H}%2B\frac{H}{2}$

External links

Definition and properties of a circular arc With interactive animation
A collection of pages defining arcs and their properties, with animated applets Arcs, arc central angle, arc peripheral angle, central angle theorem and others.
Weisstein, Eric W., "Arc" from MathWorld.
Radius of an arc or segment With interactive animation